TEOREMA DE
PITÁGORAS
Ahora bien, para
empezar a estudiar las Funciones Trigonométricas, es necesario
Dominar lo que en
Matemáticas se conoce como el Teorema de Pitágoras, para ello,
Nos familiarizaremos
con algunos de sus términos descritos a
Continuación:
En un Triángulo Rectángulo el Cuadrado de la Hipotenusa es igual a la suma
De los Cuadrados de sus Catetos”.
Demostraciones geograficas
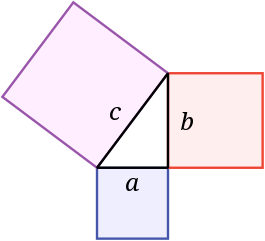
Una de las demostraciones geométricas mas conocidas, es la que se muestra a continuación, que suele atribuirse al propio Pitágoras
A partir de la igualdad de los triángulos rectángulos es evidente la igualdad
a2 + b2 = c2
PLATÓN.
La relación que expresa el teorema de Pitágoras es especialmente intuitiva si se aplica a un triángulo rectángulo e isósceles.
EUCLIDES
La relación entre los catetos y la hipotenusa de un triángulo rectángulo, aparece ya en los Elementos de Euclides.
MÉTODO DEL POLÍGONO
Éste es el método gráfico más utilizado para realizar operaciones con vectores, debido a que se pueden sumar o restar dos o más vectores a la vez.
El método consiste en colocar en secuencia los vectores manteniendo su magnitud, a escala, dirección y sentido; es decir, se coloca un vector a partir de la punta flecha del anterior. El vector resultante esta dado por el segmento de recta que une el origen o la cola del primer vector y la punta flecha del último vector.
Suma de Vectores (Metodo del Poligono)
Cuando vamos a sumar más de dos vectores , podemos sumar dos de ellos por el método del triángulo. Luego el vector resultante sumarlo con otro vector también por el método del triángulo, y así sucesivamente hasta llegar a obtener la resultante final.
Otra forma de hacer la suma , es utilizando el llamado método del polígono. Este método es simplemente la extensión del método del triángulo. Es decir, se van desplazando los vectores para colocarlos la “cabeza” del uno con la “cola” del otro (un “trencito”) y la resultante final es el vector que cierra el polígono desde la “cola” que quedo libre hasta la “cabeza” que quedo también libre (cerrar con un “choque de cabezas”). Nuevamente el orden en que se realice la suma no interesa, pues aunque el polígno resultante tiene forma diferente en cada caso, la resultante final conserva su magnitud, su dirección y su sentido.
Reglas para el método del paralelogramo
Las cantidades vectoriales no se suman como las escalares. Una velocidad de 2 Km/h sumada con otra velocidad de 3 Km/h, no necesariamente da como resultado 5 Km/h.
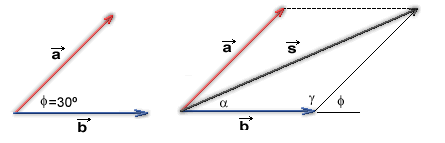
Para encontrar la resultante de dos vectores en un sistema convergente o angular con el método del paralelogramo, primero debes asegurarte de dibujar los vectores con el mismo punto de origen. Acuérdate de dibujarlos a escala.
Luego, con tus escuadras, trazas paralelas a los vectores. ¿Ves lo que construiste? Eso, que quizá te parece un rectángulo “chueco”, es un paralelogramo (que se define como un polígono de cuatro lados, paralelos dos a dos).
Como el cuadrado y el rectángulo son casos particulares del paralelogramo, habrá ocasiones, de vez en cuando, en que al trazar tus vectores y sus líneas paralelas obtengas alguna de estas dos figuras. Pero, por lo general, lo que construirás será un romboide o un rombo. Si necesitas refrescar estos conceptos geométricos, te recomiendo que leas
La resultante será la diagonal del paralelogramo que salga del punto de origen de los vectores y cuya punta de flecha (acuérdate que es un vector y por lo tanto se representa con una flecha) quede ubicada donde se cruzan las paralelas que dibujaste.
Para saber la magnitud de tu resultante, mides los centímetros que tiene y luego los conviertes a tus unidades usando tu escala… Anota también el ángulo que forma con la línea horizontal donde se encuentra el origen de los vectores y anota el sentido usando las coordenadas (N, S, E, NE, SO, SE, etc.)